Coisas em R sobre R e estatística
Comparação de 4 técnicas de seleção de modelos lineares
Por fazer...
- A técnica Forward stagewise. Só estão implementadas as técnicas forward, backward e best subset.
Intro
O código abaixo reproduz a simulação feita na página 59 do livro "Elements of Statistical Learning (2ªed)" que compara 4 abordagens de seleção de modelos lineares:
- Best Subset
- Forward Stepwise
- Backward Stepwise
- Forward Stagewise
Requisitos
library(MASS)
library(xtable)
library(bestglm)
library(ggplot2)Simulação das variáveis
Vamos fazer o passo a passo da simulação de uma resposta Y com os parâmetros definidos no livro. Depois vamos colocar tudo numa função só que gerará Y's com os parâmetros escolhidos.
Parâmetros
N <- 300
p <- 30 # supondo 31 com o intercepto
pairwiseCor <- .85 # correlação dois a dois
sdX <- matrix(pairwiseCor, p, p)
diag(sdX) <- 1
(mu <- 1:p) # vetor de médias qualquer [1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
[24] 24 25 26 27 28 29 30
sdErro <- sqrt(6.25)
BsNaoZeros <- 10 # Número de Betas diferentes de zero (menor ou igual a p)Matriz X
As p = 30 variáveis são duas a duas correlacionadas com correlação de 0.85. As médias foram arbitrariamente escolhidas.
X <- mvrnorm(n = N, mu = mu, Sigma = sdX)
# correlações
table(round(cor(X), 2))
0.8 0.81 0.82 0.83 0.84 0.85 0.86 0.87 0.88 1
4 4 46 160 228 246 140 40 2 30
X <- cbind(1, X)
dim(X)[1] 300 31Vetor \(\epsilon\)
epsilon <- rnorm(N, 0, sd = sdErro)Vetor Y
O intercepto igual a zero. Abaixo é feito o sorteio de 10 X's para ter Betas diferentes de zero.
# Betas
B <- c(rnorm(BsNaoZeros, 0, 4), rep(0, p - BsNaoZeros))[sample(p)]
B <- c(0, B) # intercepto igual a zeroTabelinha bonitinha para apresentar os valores dos parâmetros diferentes de zero e exemplificar o uso de LateX no .Rmd.
params_verdadeiros <- data.frame(Param = (sprintf("$\\beta_{%s}$",0:p)), Valor = round(B, 2))
params_verdadeiros <- params_verdadeiros[ params_verdadeiros$Valor != 0, ]
print(
xtable(params_verdadeiros),
type="html",
include.rownames=FALSE
)| Param | Valor |
|---|---|
| \(\beta_{6}\) | 3.03 |
| \(\beta_{7}\) | -0.12 |
| \(\beta_{10}\) | -1.13 |
| \(\beta_{11}\) | -1.80 |
| \(\beta_{14}\) | -0.47 |
| \(\beta_{17}\) | -2.68 |
| \(\beta_{19}\) | -3.78 |
| \(\beta_{25}\) | 3.06 |
| \(\beta_{29}\) | 0.24 |
| \(\beta_{30}\) | -5.97 |
Resposta Y
Y <- X%*%B + epsilonTranformando em função
Agora tudo que foi feito acima pode virar uma função que gera Y com os parâmetros que quisermos. Só aceita matrizes de covariância uniforme.
detalhe minúsculo: no livro está escrito que os parâmetros são sorteados de uma N(0, .4), mas eles quiseram dizer N(0, 4).
geraY <- function(N = 300,
p = 30,
mu = 1:p,
pairwiseCor = .85,
sdX = 1,
sdErro = 2.5,
BsNaoZeros = p%/%3,
sdB = 4,
intercepto = 0) {
Sigma <- sdX * matrix(pairwiseCor, p, p) + diag(p) * (1 - pairwiseCor)
X <- mvrnorm(n = N, mu = mu, Sigma = Sigma)
epsilon <- rnorm(N, 0, sd = sdErro)
B <- c(rnorm(BsNaoZeros, 0, sdB), rep(0, p - BsNaoZeros))[sample(p)]
B <- c(intercepto, B)
Y <- cbind(1, X)%*%B + epsilon
return(invisible(list(X = X,
epsilon = epsilon,
B = B,
Y = Y)))
}Simulações
Para reproduzir.
set.seed(1)As simulações ficam guardadas em uma lista. É aqui que muda os parâmetros dos modelos simulados caso queira. Basta colocar como argumento na função geraY(). O default da função é:
- N = 300
- p = 30
- mu = 1:p
- pairwiseCor = .85
- sdX = 1
- sdErro = 2.5
- BsNaoZeros = p%/%3
- sdB = 4
- intercepto = 0
n_simulacoes <- 50
simulacoes <- lapply(1:n_simulacoes, function(x) geraY())Seleção de modelos
Funções úteis
# Função que retorna um data.frame com dimensão (p+1)x(p), com a coluna 'k' contendo os coeficientes ajustados do melhor modelo de tamanho 'k'. As linhas são definidas pelos parâmetros. Os melhores modelos são selecionados pelo método 'method'. O default é "exhaustive" (best subset).
beta_dos_melhores_de_tam_k <- function(simulacao, method = "exhaustive") {
# parametros
p <- ncol(simulacao$X)
Xy <- with(simulacao, data.frame(X = X, y = Y))
selecionados <- regsubsets(y ~ ., data = Xy, nvmax=(p+1), method = method)
selecionados_bool <- summary(selecionados)
# faz ajuste para cada um dos melhores modelos de tamanho k e guarda o vetor de coeficientes
vetores_de_Bchapeu <- data.frame(sapply(1:p, function(id) {
Bchapeu <- rep(0, p+1)
Bchapeu[selecionados_bool$which[id, ]] <- coef(selecionados, id)
return(Bchapeu)
}))
return(invisible(vetores_de_Bchapeu))
}
# Função que calcula o desvio do Bchapeu em relação ao verdadeiro valor B.
desvio_do_param_verdadeiro <- function(Bchapeu, B) {
sqrt(mean((Bchapeu - B)^2))
}
# Função que devolve o desvio Bchapeu de B para cada tamanho k de uma simulação.
desvios_de_B <- function(simulacao, B, method) {
desvios <- sapply(beta_dos_melhores_de_tam_k(simulacao, method), desvio_do_param_verdadeiro, B = B)
return(desvios)
}Banco de dados dos desvios médios
BD com os desvios médios das 50 simulações para cada tamanho de modelo.
Dos 4 métodos, o forward stagewise ainda não foi feito. Ajuda é bem vinda!
metodos <- c("exhaustive", "forward", "backward")
desvio_medio <- lapply(metodos, function(metodo) {
cat(metodo)
tempo_inicial <- Sys.time()
desvio <- sapply(simulacoes, desvios_de_B, B = B, method = metodo)
desvio_medio <- rowMeans(desvio)
p <- length(desvio_medio)
desvio_medio <- data.frame(desvio_medio = desvio_medio/max(desvio_medio),
tamanho = 1:p,
method = metodo)
duracao <- Sys.time() - tempo_inicial
cat(paste0(" OK (",round(as.numeric(duracao),0)," ",attr(duracao,"units"),")\n"))
return(desvio_medio)
})exhaustive OK (27 secs)
forward OK (11 secs)
backward OK (11 secs)
desvio_medio <- do.call(rbind, desvio_medio)Resultados
ggplot(desvio_medio, aes(x = tamanho, y = desvio_medio, colour = method)) +
geom_point() +
geom_line() +
labs(x = "Tamanho",
y = expression(paste(plain(E),"||",hat(beta),"(k) - ",beta,"||")^2),
colour = "Método") +
theme_bw()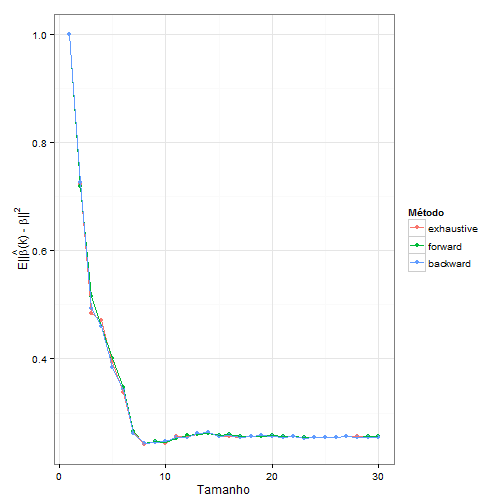
plot of chunk desvioMedioComparacao
Considerações
- Os 3 outros métodos deram resultados parecidos, mas o "best subset" demorou quase o triplo do tempo.
- O viés médio foi calculado como \[E||\hat{\beta}(k) - \beta||^2 = \frac{1}{50}\sum^{50}_{i=1}\left(\frac{1}{10}\sum^{10}_{i=1}\hat{(\beta}_i(k) - \beta_i)^2\right)\] e depois dividi pelo máximo para ficar entre 0 e 1. O problema é que não ficou como no livro. Precisa conferir se é isso mesmo.
